Difference between revisions of "Hundred dollars a kg"
| (23 intermediate revisions by 5 users not shown) | |||
| Line 5: | Line 5: | ||
==How much lifted to GEO== | ==How much lifted to GEO== | ||
| − | + | Five hundred [[gigawatt|GW]] of [[solar power satellite|power sat]]s at 2kg/kW requires 1 million tons (a billion kg) per year lifted to GEO. More likely 2.5 times that if power sat mass can't be reduced below 5kg/kW). | |
| − | Do we have to lift that much mass? No. Extra terrestrial resources are a better idea, but there isn't time to develop the space industry to tap them. The economic effects (including famines) of the developing energy crisis are so bad that the large scale production of SBSP needs to come on line | + | Do we have to lift that much mass? No. Extra terrestrial resources are a better idea, but there isn't time to develop the space industry to tap them. The economic effects (including famines) of the developing energy crisis are so bad that the large scale production of SBSP needs to come on line shortly after 2015 to avoid economic collapse. Expect ET resources to be exploited by 2025 with this much economic activity in space. |
| − | + | One million tonnes/years is in excess of 100 tonnes per hour. Will physics let us get under $100/kg? A [[moving cable space elevator]] only requires about 15 kWh to lift a kg from the surface of the earth to GEO (1.5 GW will lift 100t/hr). This is $1.50 at the high rate of 10 cents a kWh. Even if it cost $100 billion dollars to build, a capital cost of $10 billion a year lifting a billion kg is only ten dollars per kg. Unfortunately we don't have the cable – yet. | |
There are other choices but the ones further examined here are among rockets, lasers or some combination of them. | There are other choices but the ones further examined here are among rockets, lasers or some combination of them. | ||
| − | ==Rockets | + | ==Rockets or lasers?== |
| − | Rockets are good for high thrust, but the {{wpalt|Tsiolkovsky rocket equation|rocket equation}} is a hard taskmaster when you need [[delta V]] that is a multiple of the exhaust velocity. | + | Rockets are good for high thrust, but the {{wpalt|Tsiolkovsky rocket equation|rocket equation}} is a hard taskmaster when you need [[delta V]] that is a significant multiple of the exhaust velocity. |
| − | + | The root problem spaceflight has had all along is the rocket equation. All the problems flow from the fact that at best one part in 60 of the liftoff mass gets to GEO or lunar orbit. Here is the rocket equation in graphical form. | |
| − | + | [[Image:Rocket_mass_ratio_versus_delta-v.png]] | |
| − | The energy payback (for making fuel) is about 40 days<sup>'''[[/Note 1|1]]'''</sup>. The cost of rockets is not in the fuel, but in the high cost of aerospace hardware and the rocket equation which dictates that even for the most energetic fuels only about one part in sixty of the liftoff mass is payload delivered to GEO. | + | And here is what is needed in delta V. |
| − | + | ||
| − | The | + | http://en.wikipedia.org/wiki/File:Deltavs.svg |
| + | |||
| + | |||
| + | {{wpalt|laser propulsion|Laser ablation propulsion}} is not as well developed as rockets. Laser thrusters can get very high exhaust velocity, leading to small mass ratios, but they don't do very good for high thrust. {{wpalt|Jordin Kare}} and others have been working for decades designing lasers to launch from the surface. Laser launch from earth surface requires high laser power (~1 GW/ton) or results in inconveniently small payloads.. | ||
| + | |||
| + | Rockets to lift 100 t/hr would have to launch every hour, each rocket having a lift off mass of 6,000 tons to get 350 tons to LEO and 100 tons of that to GEO. The projected cost to GEO is around $500/kg, five times too expensive. http://www.ilr.tu-berlin.de/koelle/Neptun/NEP2015.pdf | ||
| + | |||
| + | The energy payback (for making fuel) is about 40 days<sup>'''[[/Note 1|1]]'''</sup>. The cost of rockets transport to GEO is not in the fuel, but in the high cost of aerospace hardware and the rocket equation which dictates that even for the most energetic fuels only about one part in sixty of the liftoff mass is payload delivered to GEO. | ||
| + | |||
| + | ==Rockets and lasers—pop up and push== | ||
| + | |||
| + | The $100/kg proposal is to combine the high thrust of rockets with the high exhaust velocity of ablation laser propulsion. It allows large payloads to be sent to GEO using relatively small lasers. The reason it works is that it matches the stage exhaust velocity to the mission velocity allowing small mass ratios. | ||
| + | |||
| + | Of the 14 km/sec needed to GEO, the rocket part of the pop up and push will provide about 2 km/sec. | ||
| + | |||
| + | (A mass ratio 3 rocket will reach its exhaust velocity, of 4k/sec, but ~2km/sec is lost to gravity and air drag.) | ||
| + | |||
| + | So the laser stage has to provide about 12 km/sec of the 14 needed to get to GEO and circularize the orbit. | ||
| + | |||
| + | For a mass ratio of 3, this would require an exhaust velocity of 12 km/sec, for a mass ratio of 2 about 17 km/sec. That's between 1/3 and 1/2 payload. The laser stage is about 1/6th the mass of the chemical stage and very simple. | ||
| + | |||
| + | Everybody who has looked at the rocket equation knows that matching delta V to the mission profile keeps the mass ratio reasonable.. The problem is that the combination of high thrust and high exhaust velocity take ferocious amounts of power to lift anything substantial. Ion engines, for example, have exhaust velocities that range up to 60 km/sec, but thrust in the milligee range--not useful if you have to do a high delta V maneuver in a hurry. | ||
| + | |||
| + | Ablation lasers have been considered for earth launch but as pointed out, they are either really huge or lift small payloads. | ||
| + | |||
| + | Using a chemical stage under a laser stage does not add much to the cost per kg because the rocket is relatively small, relatively low performance and thus can be reusable like an aircraft, i.e., fly it twice a day for 20 years. The performance of the chemical stage is low enough that a winged vehicle might do the job. | ||
| − | The power | + | The laser stage does require a substantial amount of power, 4-5 GW (equal to a ton of TNT per second). But the hang time you get from the chemical stage allows a low acceleration, just over a g, and the payload size can be in the 15-25 ton range. |
| − | + | The laser stays on the ground and is bounced from focusing mirrors in GEO. The laser stage goes around the Hohmann transfer orbit one and a half times so the laser will be in the right place to circularize its orbit to GEO. The rockets launch every 15 minutes to keep the laser busy. This provides a flow of materials to GEO of 60-100 tons per hour. | |
| − | + | That's enough materials over a few decades to replace all fossil fuels with low cost space based solar power, even liquid fuels can be made from CO2 pulled out of the air and hydrogen from water for a dollar a gallon. | |
| − | + | More detail here: | |
| − | + | http://www.nss.org/settlement/ssp/library/CO2andSpaceResources.ppt | |
| − | = | + | =First method= |
There is another way that cuts the liftoff mass by a factor of five compared to rockets. | There is another way that cuts the liftoff mass by a factor of five compared to rockets. | ||
| Line 41: | Line 66: | ||
Injection to [[geosynchronous transfer orbit]] is 7.8 k/s (to LEO), 2.5 k/s (to GTO) plus 1.6k/sec to circularize at GEO, totaling 11.9 km/s. (See [[wikipedia:Delta-v_budget|Delta-v_budget]]) To get to LEO takes 796 s at 1g, 13.2 minutes. At one g 17.5 minutes for GTO, 14 minutes at 1.25 g, plus 2.2 minutes to circularize the orbit (1.6 km/s) at GEO. Assuming half payload and half reaction mass, 0.69 velocity ratio and 11.9 km/s delta v, then the average exhaust velocity needs to be a modest (for lasers) 17.2 km/s. | Injection to [[geosynchronous transfer orbit]] is 7.8 k/s (to LEO), 2.5 k/s (to GTO) plus 1.6k/sec to circularize at GEO, totaling 11.9 km/s. (See [[wikipedia:Delta-v_budget|Delta-v_budget]]) To get to LEO takes 796 s at 1g, 13.2 minutes. At one g 17.5 minutes for GTO, 14 minutes at 1.25 g, plus 2.2 minutes to circularize the orbit (1.6 km/s) at GEO. Assuming half payload and half reaction mass, 0.69 velocity ratio and 11.9 km/s delta v, then the average exhaust velocity needs to be a modest (for lasers) 17.2 km/s. | ||
| − | Because the laser can be cycled close to 4 times an hour, the payload only needs to be 25 tons. Taking the midpoint (the exhaust velocity would be varied for constant thrust) the power required for 1.25 g (12.25 m/sec exp 2) is 1/2 x 37,500 kg x 12.25 m/sec exp 2 x 17,200 m/sec = 4 GW. In the context of building a GW of power satellite a day, this is a small piece of hardware. The choice of building the laser in space or on the ground has not been fully examined. | + | Because the laser can be cycled close to 4 times an hour, the payload only needs to be 25 tons. Taking the midpoint (the exhaust velocity would be varied for constant thrust) the power required for 1.25 g (12.25 m/sec exp 2) is 1/2 x 37,500 kg x 12.25 m/sec exp 2 x 17,200 m/sec = 4 GW. In the context of building a GW of power satellite a day, this is a small piece of hardware. |
| + | |||
| + | The choice of building the laser in space or on the ground has not been fully examined. Eventually propulsion lasers will be constructed in space. But initially it looks like building them on the ground and reflecting the laser light from a few hundred 5 ton mirrors in GEO may be the least complicated approach. As long as there is only one set of mirrors at GEO, they can be directed against targets only on the hemisphere under the mirrors. | ||
| − | The 50-ton payload-plus-reaction-mass has to hang in space long enough to be accelerated. This takes a modest mass ratio rocket. | + | The 50-ton payload-plus-reaction-mass (mass ratio 2) has to hang in space long enough to be accelerated. This takes a modest mass ratio rocket. |
{| | {| | ||
| Line 56: | Line 83: | ||
The rocket would lift off on two SSMEs (or similar), and if a zeroth turbofan stage was used, it would take eight 50-ton thrust engines, perhaps with afterburners. Simplifying operations, it goes straight up and lands back at the launching site. If the payload is oriented at right angles to vertical, we could avoid wasting time reorienting it for laser acceleration. | The rocket would lift off on two SSMEs (or similar), and if a zeroth turbofan stage was used, it would take eight 50-ton thrust engines, perhaps with afterburners. Simplifying operations, it goes straight up and lands back at the launching site. If the payload is oriented at right angles to vertical, we could avoid wasting time reorienting it for laser acceleration. | ||
| − | This "little" rocket (about the mass of a 747) has a mass ratio of | + | This "little" rocket (about the mass of a 747) has a mass ratio of three and a delta V of 4 k/sec (less gravity loss and drag). The payload-plus-reaction-mass exits the atmosphere at 2.1 k/sec, goes up to 260 miles, falls to 150 miles before picking up orbital velocity and falls to 55 miles (picking up a little air drag) before losing downward velocity. It enters GTO 1000 seconds after launch. This is conservative, not accounting for the curvature of the earth. |
[[Image:8bb60f5.jpg|thumb|Pop up and push]] | [[Image:8bb60f5.jpg|thumb|Pop up and push]] | ||
| Line 66: | Line 93: | ||
Energy payback is 8 days for the rocket fuel and 8 days for the laser. This is about 8.4% of the theoretical minimum for a [[space elevator]]. | Energy payback is 8 days for the rocket fuel and 8 days for the laser. This is about 8.4% of the theoretical minimum for a [[space elevator]]. | ||
| − | This is probably not the optimum design. A shorter "hang time," smaller payloads and higher but shorter acceleration may yield lower cost per kg. (It is possible that laser launch from the ground is the end point of this optimization.) However, the size of the largest part for a power satellite may limit the minimum size of rocket. | + | This is probably not the optimum design. A shorter "hang time," smaller payloads and higher but shorter acceleration may yield lower cost per kg. (It is possible that laser launch from the ground is the end point of this optimization.) However, the size of the largest part for a power satellite may limit the minimum size of rocket/payload. |
| + | |||
| + | The normal rule of thumb for laser propulsion from the ground is a MW/kg or a GW/tonne. Because the laser stage is not fighting gravity or air drag, "pop up and push" needs only 4 GW for a 25 tonne payload. | ||
| + | |||
| + | ==Second approach== | ||
| + | |||
| + | Getting to GEO, ~14 km/sec seems to require 2 stages. The question is "where to stage" with the practical problem of getting the first stage back to the takeoff point. By going into LEO the vehicle can be returned to the launch point after one or more orbits. | ||
| + | |||
| + | Going back to the fundamentals of the rocket equation, single stage to orbit needs about 9 km/sec average exhaust velocity. | ||
| + | |||
| + | A UK project by Reaction Engines is the Skylon. The people who designed it think they can get 12 tons into LEO. It gets up to 26 km and 2 km/sec on wings burning hydrogen and air. Back calculated from fuel consumption it has a truly remarkable 10.5 km/sec equivalent exhaust velocity. | ||
| + | |||
| + | If the vehicle swaps internal oxygen for payload and the hydrogen is heated by 6 GW of laser, then a Skylon derived vehicle should be able to put 1/3 of its takeoff mass in LEO. For a takeoff of 300 tons (smaller than the smallest 747) and a vehicle mass of 50 tons, that means each launch would put 50 tons in LEO. Again given laser heating to 3000 deg K, 35 of that 50 tons should reach GEO. Using a entirely reasonable take off rate of 3-4 per hour, this transport system would put around a million tons per year in GEO. At 5kg/kW that would build 200 GW of new plants per year. It would only take a decade or two to get the world entirely off coal and nuclear power sources. | ||
| + | |||
| + | A variant of this concept was reported here: http://www.foxnews.com/scitech/2011/01/25/nasa-exploring-lasers-beams-zap-rockets-outer-space/ | ||
| + | |||
| + | ==Geometry issues== | ||
| + | |||
| + | The long acceleration required for relatively low laser power means the laser needs to track the vehicle across several thousand km of the Earth's equator. The obvious approach is to place redirection mirrors in GEO, send the laser beam up to them and have the mirrors track the vehicle as it accelerates into LEO. | ||
| + | |||
| + | This means the lasers need to be 30-40 deg to the east of the takeoff point. There are not many combination of takeoff locations on the equator and locations where 10-12 GW of power can be drawn from the grid. | ||
| + | |||
| + | The US has one of them, Jarvis island for the takeoff and Sylmar or some other location on the Pacific Intertie for the lasers. | ||
| + | |||
| + | The Maldives and Three Gorges Dam would work for China. | ||
| + | |||
| + | Brazil and Spain or Portugal are another. | ||
| + | |||
| + | Somalia and a location in India would work, but the grid infrastructure is light in India. | ||
| + | |||
| + | ==Other uses for a laser== | ||
| + | |||
| + | There is an awful lot of space junk, 15,000 pieces at least. Power satellites built in LEO and tranported to GEO on high impulse engines have been proposed. Even back in the late 1970s when there was a lot less space junk it was realize that something the size of a power sat would arrive at GEO full of holes. A propulsion laser can be used to deorbit space junk. | ||
| + | |||
| + | ==Other low cost ways to GEO== | ||
| + | |||
| + | Pop up and push is not the only approach that could reduced the cost of transport to GEO down to $100/kg. Another approach is to hang a partial elevator, ending an earth diameter or so from the surface and use rockets to reach the low end of the elevator. Existing materials such as Spectra are strong enough for a partial elevator. The energy reduction is reported to be about 75% compared to going into LEO. The cost reduction would be better than 75%. Since the most optimistic numbers for going into LEO are about $300/kg, this could result in cargo to GEO for about $100/kg. | ||
| + | |||
| + | Next [[Miller's method]] to fund power sats. | ||
Latest revision as of 12:34, 15 March 2011
To sum up what's gone before: Dollar a gallon gasoline .. Penny a kWh electricity.
To solve the energy crisis using space-based solar power, replacement power needs to come on line at a rate of 400-500 GW/year. That replaces about 6 million barrels of oil a day each year over the next 50 years. To make liquid fuels at a dollar a gallon out of electricity requires that the electricity cost be around a penny a kWh. To make penny a kWh requires lift cost to GEO of $100 or less
How much lifted to GEO
Five hundred GW of power sats at 2kg/kW requires 1 million tons (a billion kg) per year lifted to GEO. More likely 2.5 times that if power sat mass can't be reduced below 5kg/kW).
Do we have to lift that much mass? No. Extra terrestrial resources are a better idea, but there isn't time to develop the space industry to tap them. The economic effects (including famines) of the developing energy crisis are so bad that the large scale production of SBSP needs to come on line shortly after 2015 to avoid economic collapse. Expect ET resources to be exploited by 2025 with this much economic activity in space.
One million tonnes/years is in excess of 100 tonnes per hour. Will physics let us get under $100/kg? A moving cable space elevator only requires about 15 kWh to lift a kg from the surface of the earth to GEO (1.5 GW will lift 100t/hr). This is $1.50 at the high rate of 10 cents a kWh. Even if it cost $100 billion dollars to build, a capital cost of $10 billion a year lifting a billion kg is only ten dollars per kg. Unfortunately we don't have the cable – yet.
There are other choices but the ones further examined here are among rockets, lasers or some combination of them.
Rockets or lasers?
Rockets are good for high thrust, but the rocket equation[W] is a hard taskmaster when you need delta V that is a significant multiple of the exhaust velocity.
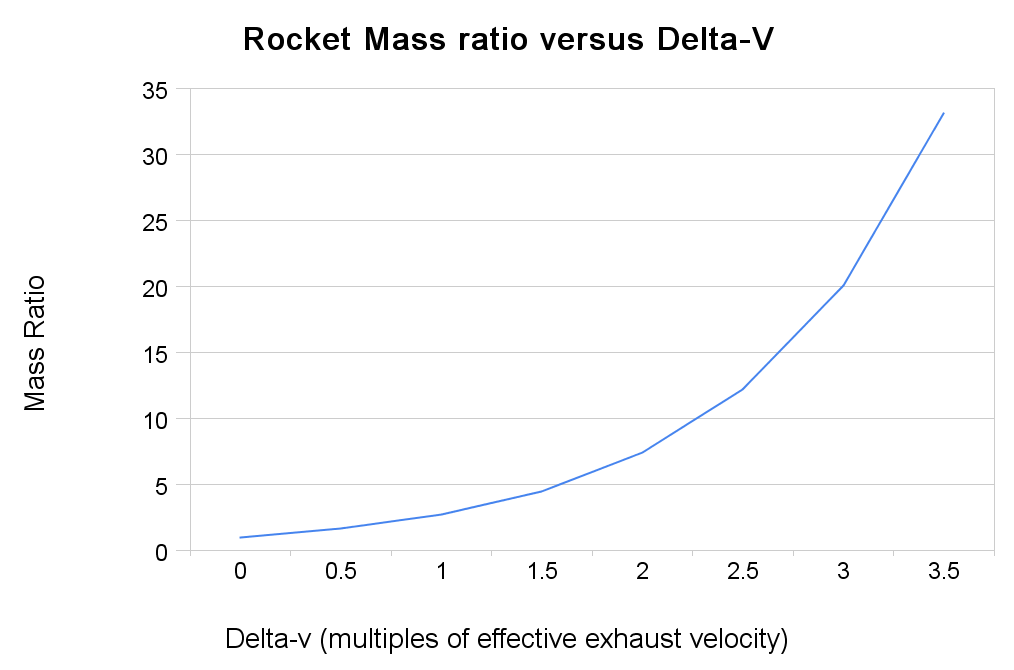
The root problem spaceflight has had all along is the rocket equation. All the problems flow from the fact that at best one part in 60 of the liftoff mass gets to GEO or lunar orbit. Here is the rocket equation in graphical form.
And here is what is needed in delta V.
http://en.wikipedia.org/wiki/File:Deltavs.svg
Laser ablation propulsion[W] is not as well developed as rockets. Laser thrusters can get very high exhaust velocity, leading to small mass ratios, but they don't do very good for high thrust. Jordin Kare[W] and others have been working for decades designing lasers to launch from the surface. Laser launch from earth surface requires high laser power (~1 GW/ton) or results in inconveniently small payloads..
Rockets to lift 100 t/hr would have to launch every hour, each rocket having a lift off mass of 6,000 tons to get 350 tons to LEO and 100 tons of that to GEO. The projected cost to GEO is around $500/kg, five times too expensive. http://www.ilr.tu-berlin.de/koelle/Neptun/NEP2015.pdf
The energy payback (for making fuel) is about 40 days1. The cost of rockets transport to GEO is not in the fuel, but in the high cost of aerospace hardware and the rocket equation which dictates that even for the most energetic fuels only about one part in sixty of the liftoff mass is payload delivered to GEO.
Rockets and lasers—pop up and push
The $100/kg proposal is to combine the high thrust of rockets with the high exhaust velocity of ablation laser propulsion. It allows large payloads to be sent to GEO using relatively small lasers. The reason it works is that it matches the stage exhaust velocity to the mission velocity allowing small mass ratios.
Of the 14 km/sec needed to GEO, the rocket part of the pop up and push will provide about 2 km/sec.
(A mass ratio 3 rocket will reach its exhaust velocity, of 4k/sec, but ~2km/sec is lost to gravity and air drag.)
So the laser stage has to provide about 12 km/sec of the 14 needed to get to GEO and circularize the orbit.
For a mass ratio of 3, this would require an exhaust velocity of 12 km/sec, for a mass ratio of 2 about 17 km/sec. That's between 1/3 and 1/2 payload. The laser stage is about 1/6th the mass of the chemical stage and very simple.
Everybody who has looked at the rocket equation knows that matching delta V to the mission profile keeps the mass ratio reasonable.. The problem is that the combination of high thrust and high exhaust velocity take ferocious amounts of power to lift anything substantial. Ion engines, for example, have exhaust velocities that range up to 60 km/sec, but thrust in the milligee range--not useful if you have to do a high delta V maneuver in a hurry.
Ablation lasers have been considered for earth launch but as pointed out, they are either really huge or lift small payloads.
Using a chemical stage under a laser stage does not add much to the cost per kg because the rocket is relatively small, relatively low performance and thus can be reusable like an aircraft, i.e., fly it twice a day for 20 years. The performance of the chemical stage is low enough that a winged vehicle might do the job.
The laser stage does require a substantial amount of power, 4-5 GW (equal to a ton of TNT per second). But the hang time you get from the chemical stage allows a low acceleration, just over a g, and the payload size can be in the 15-25 ton range.
The laser stays on the ground and is bounced from focusing mirrors in GEO. The laser stage goes around the Hohmann transfer orbit one and a half times so the laser will be in the right place to circularize its orbit to GEO. The rockets launch every 15 minutes to keep the laser busy. This provides a flow of materials to GEO of 60-100 tons per hour.
That's enough materials over a few decades to replace all fossil fuels with low cost space based solar power, even liquid fuels can be made from CO2 pulled out of the air and hydrogen from water for a dollar a gallon.
More detail here:
http://www.nss.org/settlement/ssp/library/CO2andSpaceResources.ppt
First method
There is another way that cuts the liftoff mass by a factor of five compared to rockets.
Injection to geosynchronous transfer orbit is 7.8 k/s (to LEO), 2.5 k/s (to GTO) plus 1.6k/sec to circularize at GEO, totaling 11.9 km/s. (See Delta-v_budget) To get to LEO takes 796 s at 1g, 13.2 minutes. At one g 17.5 minutes for GTO, 14 minutes at 1.25 g, plus 2.2 minutes to circularize the orbit (1.6 km/s) at GEO. Assuming half payload and half reaction mass, 0.69 velocity ratio and 11.9 km/s delta v, then the average exhaust velocity needs to be a modest (for lasers) 17.2 km/s.
Because the laser can be cycled close to 4 times an hour, the payload only needs to be 25 tons. Taking the midpoint (the exhaust velocity would be varied for constant thrust) the power required for 1.25 g (12.25 m/sec exp 2) is 1/2 x 37,500 kg x 12.25 m/sec exp 2 x 17,200 m/sec = 4 GW. In the context of building a GW of power satellite a day, this is a small piece of hardware.
The choice of building the laser in space or on the ground has not been fully examined. Eventually propulsion lasers will be constructed in space. But initially it looks like building them on the ground and reflecting the laser light from a few hundred 5 ton mirrors in GEO may be the least complicated approach. As long as there is only one set of mirrors at GEO, they can be directed against targets only on the hemisphere under the mirrors.
The 50-ton payload-plus-reaction-mass (mass ratio 2) has to hang in space long enough to be accelerated. This takes a modest mass ratio rocket.
| 50 tons payload plus reaction mass for the laser | 16.5% |
| 50 tons rocket structure | 16.5% |
| 200 tons propellant. | 66% |
The rocket would lift off on two SSMEs (or similar), and if a zeroth turbofan stage was used, it would take eight 50-ton thrust engines, perhaps with afterburners. Simplifying operations, it goes straight up and lands back at the launching site. If the payload is oriented at right angles to vertical, we could avoid wasting time reorienting it for laser acceleration.
This "little" rocket (about the mass of a 747) has a mass ratio of three and a delta V of 4 k/sec (less gravity loss and drag). The payload-plus-reaction-mass exits the atmosphere at 2.1 k/sec, goes up to 260 miles, falls to 150 miles before picking up orbital velocity and falls to 55 miles (picking up a little air drag) before losing downward velocity. It enters GTO 1000 seconds after launch. This is conservative, not accounting for the curvature of the earth.
It masses 1/20th of a Neptune and (with the aid of the laser) delivers 1/4 as much payload per launch. One part in 12 (rather than one part in 60) is payload. To keep the laser busy and to meet the 100-ton per hour cargo requirement requires a launch every 15 minutes (or every 7.5 minutes for 200 tons per day). This rate is common for airlines, but not for spacecraft.
If the laser cost 40 billion dollars and was written off at 10% per year, the lift cost from sub orbital to GEO would be $4 billion /0.8 billion kg, $5/kg plus the sub orbital flight of perhaps $60/kg of payload. This reaches the penny a kWh and dollar a gallon fuel goals.
Energy payback is 8 days for the rocket fuel and 8 days for the laser. This is about 8.4% of the theoretical minimum for a space elevator.
This is probably not the optimum design. A shorter "hang time," smaller payloads and higher but shorter acceleration may yield lower cost per kg. (It is possible that laser launch from the ground is the end point of this optimization.) However, the size of the largest part for a power satellite may limit the minimum size of rocket/payload.
The normal rule of thumb for laser propulsion from the ground is a MW/kg or a GW/tonne. Because the laser stage is not fighting gravity or air drag, "pop up and push" needs only 4 GW for a 25 tonne payload.
Second approach
Getting to GEO, ~14 km/sec seems to require 2 stages. The question is "where to stage" with the practical problem of getting the first stage back to the takeoff point. By going into LEO the vehicle can be returned to the launch point after one or more orbits.
Going back to the fundamentals of the rocket equation, single stage to orbit needs about 9 km/sec average exhaust velocity.
A UK project by Reaction Engines is the Skylon. The people who designed it think they can get 12 tons into LEO. It gets up to 26 km and 2 km/sec on wings burning hydrogen and air. Back calculated from fuel consumption it has a truly remarkable 10.5 km/sec equivalent exhaust velocity.
If the vehicle swaps internal oxygen for payload and the hydrogen is heated by 6 GW of laser, then a Skylon derived vehicle should be able to put 1/3 of its takeoff mass in LEO. For a takeoff of 300 tons (smaller than the smallest 747) and a vehicle mass of 50 tons, that means each launch would put 50 tons in LEO. Again given laser heating to 3000 deg K, 35 of that 50 tons should reach GEO. Using a entirely reasonable take off rate of 3-4 per hour, this transport system would put around a million tons per year in GEO. At 5kg/kW that would build 200 GW of new plants per year. It would only take a decade or two to get the world entirely off coal and nuclear power sources.
A variant of this concept was reported here: http://www.foxnews.com/scitech/2011/01/25/nasa-exploring-lasers-beams-zap-rockets-outer-space/
Geometry issues
The long acceleration required for relatively low laser power means the laser needs to track the vehicle across several thousand km of the Earth's equator. The obvious approach is to place redirection mirrors in GEO, send the laser beam up to them and have the mirrors track the vehicle as it accelerates into LEO.
This means the lasers need to be 30-40 deg to the east of the takeoff point. There are not many combination of takeoff locations on the equator and locations where 10-12 GW of power can be drawn from the grid.
The US has one of them, Jarvis island for the takeoff and Sylmar or some other location on the Pacific Intertie for the lasers.
The Maldives and Three Gorges Dam would work for China.
Brazil and Spain or Portugal are another.
Somalia and a location in India would work, but the grid infrastructure is light in India.
Other uses for a laser
There is an awful lot of space junk, 15,000 pieces at least. Power satellites built in LEO and tranported to GEO on high impulse engines have been proposed. Even back in the late 1970s when there was a lot less space junk it was realize that something the size of a power sat would arrive at GEO full of holes. A propulsion laser can be used to deorbit space junk.
Other low cost ways to GEO
Pop up and push is not the only approach that could reduced the cost of transport to GEO down to $100/kg. Another approach is to hang a partial elevator, ending an earth diameter or so from the surface and use rockets to reach the low end of the elevator. Existing materials such as Spectra are strong enough for a partial elevator. The energy reduction is reported to be about 75% compared to going into LEO. The cost reduction would be better than 75%. Since the most optimistic numbers for going into LEO are about $300/kg, this could result in cargo to GEO for about $100/kg.
Next Miller's method to fund power sats.